Suites Arithmétiques et Géométriques - cours de math 1ère
Définition générale d’une suite
Qu’est ce qu’une suite?
Une suite est une application de N dans R. Tout comme dans les fonctions, on calcule le résultat, noté U(n) en fonction de n, la seule différence est que n peut être seulement un entier naturel.
Avec une fonction, l’inconnue est noté x, avec les suites c’est n.
U(n), en revanche, est un Réel. Les images de la suite U(n) sont appelées termes de la suite.
Formule explicite d’une suite
Une suite peut être définie par sa formule explicite. C’est une équation qui permet de calculer la valeur du terme Un en connaissant seulement n, indépendamment des autres termes de la suite.
Par exemple:
Remarque: les suites sont des applications qui le prennent leurs valeurs que dans N (les entiers).
Dans cet exemple, on utilisa la formule explicite pour calculer les termes de U:
La formule s’applique à chacun des entiers n
Formule par récurrence d’une suite
On peut également définir une suite par récurrence. Chaque terme se calcule en fonction du précédent.
En connaissant le premier terme de la suite et la formule qui permet de calculer le suivant, on peut calculer tous les termes de la suite:
Dans cet exemple, on ajoute 1 à chaque fois pour passer au terme suivant. Il ‘agit de la même quite que dans l’exemple précédent, mais représentée par sa formule par récurrence.
Suite arithmétique
Définition d’une suite arithmétique
On appelle suite arithmétique une suite où pour passer d’un terme au suivant, on ajoute toujours la même valeur r.
r est appelé raison de la suite, et est un nombre Réel.
Exemple de suite arithmétique
Dans l’exemple précédent, la suite présentée est une suite arithmétique. On remarque que graphiquement, elle a la forme d’un escalier dont les marches sont régulières (car r ne change pas).
Formule explicite d’une suite arithmétique
On peut retrouver la formule explicite d’une suite arithmétique de la manière suivante:
Si:
Alors:
Comme on ajoute r pour passer d’un terme au suivant, lorsqu’on est au terme de rang n, on a ajouté n fois r au terme de rang 0.
Il n’est pas nécessaire de connaitre Uo, on peut calculer Un en fonction de n’importe quel terme connu de rang p:
Suite géométrique
Définition d’une suite géométrique
On appelle suite géométrique une suite où pour passer d’un terme au suivant, on le multiplie par r.
r est la raison de la suite, est est un nombre réel.
Exemple de suite géométrique
La suite suivante est une suite géométrique de raison 1/2. Pour passer d’un terme au suivant, on le multiplie par 1/2, ce qui revient sur le graphique à diviser la hauteur par 2 à chaque passage au terme suivant.
Formule explicite d’une suite géométrique
On peut retrouver la formule explicite d’une suite géométrique de la manière suivante:
Si:
Alors:
Comme on multiplie par r pour passer d’un terme au suivant, lorsqu’on est au terme de rang n, on a multiplié n fois par r le terme de rang 0.
Il n’est pas nécessaire de connaître Uo, on peut calculer Un en fonction de n’importe que terme connu de rang p:
Suite arithmético-géométrique
Une suite arithmético-géométrique est un mélange entre les deux types de suites précédentes. Cela signifie que pour passer d’un terme au suivant, on le multiplie par une raison r2, et on ajoute une autre raison r1.
Sens de variation d’une suite
Définition du sens de variation d’une suite
Une suite Un est strictement croissante si:
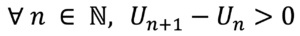
Une suite Un est croissante si:
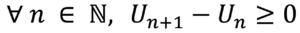
Une suite Un est strictement décroissante si:
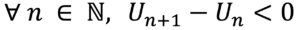
Une suite Un est strictement décroissante si:
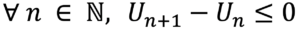
Pour savoir si une suite est croissante ou décroissante, on s’intéresse à l’écart entre deux termes successifs de la suite, qui se traduit algébriquement par la différence. On étudie l’écart quel que soit n, car une suite peut être à la fois croissante sur certains intervalles de n et décroissante sur d’autres.
Exemple de calcul su sens de variation
Dans l’exemple suivant, il est évident d’après le graphique que la suite est strictement croissante, mais on peut aussi le démontrer facilement par le calcul:
Soit la suite définie par la formule suivante:
On calcule l’écart entre Un+1 et Un, en remplaçant Un+1 par son expression en fonction de Un:
On obtient le résultat 2, qui est supérieur à 0, donc la suite est strictement croissante quel que soit n.
Limite d’une suite
Une suite est convergente vers un nombre réel L si tout intervalle ouvert contenant L contient tous les termes de la suite à partir d’un certain rang.
Le nombre L est la limite de la suite Un, notée:
Suite majorée et minorée
Une suite Un est majorée si et seulement si Un est croissante et il existe un réel a tel que Un<a pour tout n appartient à N
Une suite Un est minorée si et seulement si Un est décroissante et il existe un réel a tel que Un>a pour tout n appartenant à N
Démonstration par récurrence
Lorsqu’on connait les termes s’une suite et qu’on souhaite connaître la formule explicite de la suite, il est possible d’utiliser la méthode de la démonstration par récurrence.
Cette méthode consiste